洛谷 P10773 [NOISG 2021 Qualification] Truck 题解

2025/3/14 OI 题解线段树轻重链剖分

前言

随机跳题跳到的。我并不会题解区另外两篇大佬的做法，我用了一种相对更加复杂的拆式子。但似乎这种拆式子的方法更为通用一些？
题意题面已经很简洁了，注意一下是先减少价值，再产生费用就行了。
但我有一个问题：为什么说数据保证 \(1\le D_{i},T_{i},G\le 10^{9}\)，但是样例二，Sub1，Sub2 又存在 \(T_{i}=0\)？

思路

首先我们令 \(dis(x,y)\) 表示从 \(x\) 到 \(y\) 经过的边的 \(T_{i}\) 和。\(D_{i}\) 在边上不好做，我们使用边权转点权，将一条边的 \(D_{i}\) 的值，放到这条边相连的两个点中，深度更深的那个上面。

记 \(S(x,y)\) 表示从 \(x\) 到 \(y\) 的点集。
根据题意，我们可以写出这样的式子：

\[ ans=\left(\sum_{i\in S(x,\operatorname{LCA}(x,y)),i\not=\operatorname{LCA}(x,y)}D_{i}(dis(fa_{i},y)+G)\right)+\left(\sum_{i\in S(\operatorname{LCA}(x,y),y),i\not=\operatorname{LCA}(x,y)}D_{i}(dis(i,y)+G)\right)\\ \]

没有看懂式子的话，可以画一下图，模拟一下。

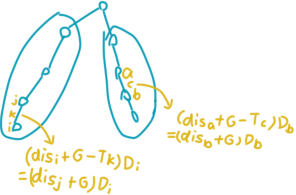
看着十分吓人，我们可以先将 \(G\) 提出来，再将 \(dis(x,y)\) 展开成 \(dep_{x}+dep_{y}-2dep_{\operatorname{LCA}(x,y)}\)。

对于 \(i\in S(x,\operatorname{LCA}(x,y))\)，都有 \(\operatorname{LCA}(i,y)=\operatorname{LCA}(x,y)\)。
对于 \(i\in S(\operatorname{LCA}(x,y),y)\) 都有 \(\operatorname{LCA}(i,y)=i\)。

那么我们便可以写成这样的式子：

\[ ans=\left(G\sum_{i\in S(x,y),i\not=\operatorname{LCA}(x,y)}D_{i}\right)+\left(\sum_{i\in S(x,\operatorname{LCA}(x,y)),i\not=\operatorname{LCA}(x,y)}D_{i}(dep_{fa_{i}}+dep_{y}-2dep_{\operatorname{LCA}(x,y)})\right)+\left(\sum_{i\in S(\operatorname{LCA}(x,y),y),i\not=\operatorname{LCA}(x,y)}D_{i}(dep_{y}-dep_{i})\right) \]

化简一下，得到：

\[ ans=\left(\left(G+dep_{y}\right)\sum_{i\in S(x,y),i\not=LCA(x,y)}D_{i}\right)+\left(\sum_{i\in S(x,LCA(x,y)),i\not=LCA(x,y)}D_{i}dep_{fa_{i}}\right)-\left(2dep_{LCA(x,y)}\sum_{i\in S(x,LCA(x,y)),i\not=LCA(x,y)}D_{i}\right)-\left(\sum_{i\in S(LCA(x,y),y),i\not=LCA(x,y)}D_{i}dep_{i}\right)\\ \]

我们发现这些都是可以使用线段树来维护的。
我们需要维护的也就是：

区间 \(D_{i}\) 和
区间 \(dep_{i}\) 和
区间 \(D_{i}dep_{i}\) 和
区间 \(D_{i}dep_{fa_{i}}\) 和

第一个是不变的。
第二个我们发现和 \(T_{i}\) 有关，而修改一条边 \(x\) 到 \(y\)（设 \(y\) 点更深）的边权为 \(t\) 后，会对 \(y\) 及其子树的 \(dep_{i}\) 一起增加 \(t-T_{i}\)（\(T_{i}\) 为改之前的边权）。这是一个区间加的操作。
第三个可以看作维护 \(kx,x=\sum dep_{i}\) 也就是增加倍数的操作。
第四个和第三个一样，因为我们每次修改的时候，会对一整棵子树进行修改，所以 \(fa_{i}\) 没变的只有这棵子树的根，特殊处理一下就行了。

那么到这里就结束了，维护起来还是有一点麻烦的。

代码

我打的比较丑陋，但是有一些注释。

// Problem: P10773 [NOISG 2021 Qualification] Truck
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P10773
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+10;
const int mod=1e9+7;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

int n,g,k,q,cnt,head[MAXN],Dep[MAXN],val[MAXN],hson[MAXN]；
int dfsnum[MAXN],dfsnod[MAXN],top[MAXN],fa[MAXN],dep[MAXN],siz[MAXN];
map<pair<int,int>,int> mp;
struct node{
    int to,next,val1,val2;
}edge[MAXN<<1];
struct node2{
    int l,r,val1,val2,val3,val4,lazy;
}tree[MAXN<<2];

void build(int u,int v,int d,int t){
    edge[++k].to=v;
    edge[k].next=head[u];
    edge[k].val1=t;
    edge[k].val2=d;
    head[u]=k;
}

void dfs(int u,int f){
    siz[u]=1;
    int maxsiz=0;
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(v==f) continue;
        fa[v]=u;
        dep[v]=(dep[u]+edge[i].val1)%mod;
        Dep[v]=Dep[u]+1;
        //因为T_i可能为0，所以额外记录一下深度。
        val[v]=edge[i].val2;
        dfs(v,u);
        siz[u]+=siz[v];
        if(maxsiz<siz[v]){
            maxsiz=siz[v];
            hson[u]=v;
        }
    }
}

void dfs2(int u,int f){
    top[u]=f;
    dfsnum[u]=++cnt;
    dfsnod[cnt]=u;
    if(hson[u]==0) return;
    dfs2(hson[u],f);
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(v==fa[u]||v==hson[u]) continue;
        dfs2(v,v);
    }
}

void pushup(int id){
    tree[id].val1=(tree[id*2].val1+tree[id*2+1].val1)%mod;
    tree[id].val2=(tree[id*2].val2+tree[id*2+1].val2)%mod;
    tree[id].val3=(tree[id*2].val3+tree[id*2+1].val3)%mod;
    tree[id].val4=(tree[id*2].val4+tree[id*2+1].val4)%mod;
}

void pushdown(int id){
    if(tree[id].lazy==0) return;
    tree[id*2].val2+=tree[id].lazy;
    tree[id*2].val3+=tree[id*2].val1*(tree[id].lazy%mod)%mod;
    tree[id*2].val4+=tree[id*2].val1*(tree[id].lazy%mod)%mod;
    tree[id*2].lazy+=tree[id].lazy;
    tree[id*2].val2%=mod;
    tree[id*2].val3%=mod;
    tree[id*2].val4%=mod;
    tree[id*2+1].val2+=tree[id].lazy;
    tree[id*2+1].val3+=tree[id*2+1].val1*(tree[id].lazy%mod)%mod;
    tree[id*2+1].val4+=tree[id*2+1].val1*(tree[id].lazy%mod)%mod;
    tree[id*2+1].lazy+=tree[id].lazy;
    tree[id*2+1].val2%=mod;
    tree[id*2+1].val3%=mod;
    tree[id*2+1].val4%=mod;
    tree[id].lazy=0;
}

void build_tree(int id,int l,int r){
    tree[id].l=l;
    tree[id].r=r;
    tree[id].lazy=0;
    tree[id].val1=tree[id].val2=tree[id].val3=tree[id].val4=0;
    if(l==r){
        tree[id].val1=val[dfsnod[l]];
        tree[id].val2=dep[dfsnod[l]];
        tree[id].val3=tree[id].val1*dep[dfsnod[l]]%mod;
        tree[id].val4=tree[id].val1*dep[fa[dfsnod[l]]]%mod;
        return;
    }
    int mid=(l+r)>>1;
    build_tree(id*2,l,mid);
    build_tree(id*2+1,mid+1,r);
    pushup(id);
}

void update(int id,int l,int r,int L,int R,int z,bool kind){
    if(r<L||R<l) return;
    if(L<=l&&r<=R){
        if(kind) tree[id].val2=(tree[id].val2+z)%mod;
        if(kind) tree[id].val3=(tree[id].val3+tree[id].val1*z%mod)%mod;
        tree[id].val4=(tree[id].val4+tree[id].val1*z%mod)%mod;
        if(kind) tree[id].lazy+=z;
        return;
    }
    pushdown(id);
    int mid=(l+r)>>1;
    if(L<=mid) update(id*2,l,mid,L,R,z,kind);
    if(R>mid) update(id*2+1,mid+1,r,L,R,z,kind);
    pushup(id);
}

int query(int id,int l,int r,int L,int R,int type){
    if(r<L||R<l) return 0;
    if(L<=l&&r<=R){
        if(type==1) return tree[id].val1;
        if(type==2) return tree[id].val2;
        if(type==3) return tree[id].val3;
        if(type==4) return tree[id].val4;
    }
    pushdown(id);
    int res=0,mid=(l+r)>>1;
    if(L<=mid){
        int val=query(id*2,l,mid,L,R,type);
        res=(res+val)%mod;
    }
    if(R>mid){
        int val=query(id*2+1,mid+1,r,L,R,type);
        res=(res+val)%mod;
    }
    return res;
}

int ask(int x,int y,int type){
    int res=0;
    while(top[x]!=top[y]){
        if(Dep[top[x]]<Dep[top[y]]) swap(x,y);
        res=(res+query(1,1,cnt,dfsnum[top[x]],dfsnum[x],type))%mod;
        x=fa[top[x]];
    }
    if(Dep[x]<Dep[y]) swap(x,y);
    res=(res+query(1,1,cnt,dfsnum[y],dfsnum[x],type))%mod;
    return res;
}

int lca(int x,int y){
    while(top[x]!=top[y]){
        if(Dep[top[x]]<Dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    if(Dep[x]<Dep[y]) swap(x,y);
    return y;
}

int work(int x,int y){
    //照着式子计算即可。
    int res=0,lc=lca(x,y);
    int sum=(g+query(1,1,cnt,dfsnum[y],dfsnum[y],2))%mod;
    int val=(ask(x,y,1)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],1)+mod)%mod;
    res=(res+sum*val%mod)%mod;
    res=(res+ask(x,lc,4)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],4)+mod)%mod;
    res-=2ll*query(1,1,cnt,dfsnum[lc],dfsnum[lc],2)%mod*
    ((ask(x,lc,1)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],1)+mod)%mod)%mod;
    res=(res+mod)%mod;
    res-=(ask(lc,y,3)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],3)+mod)%mod;
    res=(res+mod)%mod;
    return (res+mod)%mod;
}

signed main(){
    read(n,g);
    for(int i=1;i<n;i++){
        int a,b,d,t;
        read(a,b,d,t);
        build(a,b,d,t);
        build(b,a,d,t);
        mp[make_pair(a,b)]=mp[make_pair(b,a)]=t;
    }
    dfs(1,1);
    dfs2(1,1);
    build_tree(1,1,cnt);
    read(q);
    for(int i=1;i<=q;i++){
        int opt,x,y,t;
        read(opt);
        if(opt==0){
            read(x,y,t);
            if(Dep[x]<Dep[y]) swap(x,y);
            int val=t-mp[make_pair(x,y)];
            mp[make_pair(x,y)]=mp[make_pair(y,x)]=t;
            update(1,1,cnt,dfsnum[x],dfsnum[x]+siz[x]-1,val,true);
            update(1,1,cnt,dfsnum[x],dfsnum[x],-val,false);
            //只有x这个点的父亲没有修改，单独处理。
        }
        if(opt==1){
            read(x,y);
            cout<<work(x,y)<<'\n';
        }
    }
    return 0;
}

LOADING

洛谷 P10773 [NOISG 2021 Qualification] Truck 题解

前言

思路

代码