ABC375G 题解

2024/10/13 OI 题解 Tarjan 最短路

人生中第一次场切 G 题
这次的 ABC 似乎有点太简单了？
题目传送门

题意简述

给定一张 \(n\) 个点，\(m\) 条边的有权无向图，对每条边进行询问，当前询问的是第 \(i (1 \le i \le m)\) 条边，询问如下：

令 \(dis\) 为从 \(1\) 号点到 \(n\) 号点的最短路长度，
令 \(dis'\) 为删掉第 \(i\) 条边后的最短路长度，
若 \(dis \not ={dis'}\) 则输出 Yes，否则输出 No。

（若原本可以到达，现在不可以到达也输出 Yes。）
每次询问独立。

数据范围：

\(2 \le n \le 2 \times 10^{5}\)
\(1 \le m \le 2 \times 10^{5}\)

思路

因为 \(m\) 最大可以到 \(2 \times 10^{5}\)，假如每次都暴力做，每次去掉一条边，重新建图，跑一次最短路，再检查是否相等，视实现方法不同，时间复杂度会是 \(O(mn^{2})\)，\(O(m^{2}\log{m})\) 以及其他复杂度，这显然是没法通过的，我们需要更优的方法。

我们来看这个样例：

建出图后长这样：（这里我用红色标注边权）

很明显，从 \(1\) 号点到 \(n\) 号点的最短路为 \(2\)，而且不止有一条从 \(1\) 到 \(n\) 的路径的长度为 \(2\)。
我们将所有从 \(1\) 到 \(n\) 的长度为 \(2\) 的路径拿出来，是这样的：

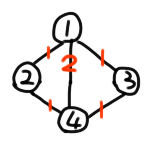
我们可以从中发现，如果一条边不在所有最短路径上，那么将这条边删去后，最短路的值不会发生变化。
那么如果在最短路上呢？

再来看一个样例：

很显然，连边后是这样的：

也很显然的，从 \(1\) 号点到 \(n\) 号点的最短路为 \(3\)，将所有最短路径拿出来后的图也是长这样的。

发现将 \((1,2),(2,4),(1,3),(3,4)\) 这几条边删去后，并不会影响最短路的长度。
而将 \((4,5)\) 这条边删去后，就直接变得不连通了。

而这样删去后，会对答案造成影响的，是什么样的边呢？
其实就是所有最短路径都必须要经过的边，也就是所有最短路径构成的一张新图（这张图也叫做最短路图）中的割边。
而更一般的，删去这些割边中的一条或者多条后，要么使得两点不连通，要么使新的最短路变大。

那现在思路就很明确了，先找到所有的最短路径，再找最短路图中的割边即可。
如果一条边是割边，那么删去后最短路就会发生变化，也就该输出 Yes。否则的话，就不会发生变化，也就输出 No。

时间复杂度会在实现的部分分析。

实现

我们首先需要找出所有的最短路径，这是容易的。

我们首先求出 \(1\) 号点到所有点的最短路，记为 \(dis_{1,i}\)。
再求出从 \(n\) 号点到所有点的最短路，记为 \(dis_{n,i}\)。
这一部分可以使用任何优化（比如优先队列优化，堆优化）过的 Dijkstra 算法。（大概率是会卡 SPFA 的）
这会是 \(O(m \log m)\) 或是 \(O(n \log n)\) 之类的。（根据具体的实现方法不同）下面就以我写的优先队列优化的为例。

接下来遍历所有的边，设当前遍历的边为第 \(i\) 条边，这条边的两个端点分别是 \(u\) 和 \(v\)，这条边的边权是 \(w\)。
若 \(dis_{1,u} + dis_{n,v} + w = dis_{1,n}\)，第 \(i\) 条边就是所有最短路径中的一条边。
因为这里是无向边，所以当 \(dis_{1,v} + dis_{n,u} + w = dis_{1,n}\) 时，第 \(i\) 条边也是所有最短路径中的一条边。
（若是有向边，就要注意一下方向的问题了）
这一部分是 \(O(m)\) 的。

我们建出这一个新图后，再找出图中的所有割边就行啦，这一部分可以使用 Tarjan 来实现，时间复杂度会是 \(O(n+m)\) 的。

总的时间复杂度是 \(O(m \log m)\) 的，可以轻松通过。

代码

// Problem: G - Road Blocked 2
// Contest: AtCoder - Panasonic Programming Contest 2024（AtCoder Beginner Contest 375）
// URL: https://atcoder.jp/contests/abc375/tasks/abc375_g
// Memory Limit: 1024 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e5+10;
const int mod1=1e9+7;
const int mod2=998244353;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

int n,m,k,k2,head[MAXN],head2[MAXN],dis[2][MAXN],y[MAXN<<1];
int low[MAXN],dfn[MAXN],times;
bool vis[MAXN],cut_edge[MAXN<<1];
struct node{
    int to,next,val;
}edge[MAXN<<1],edge2[MAXN<<1];

struct node2{
    int to,val;
    friend bool operator < (node2 n1,node2 n2){
        return n1.val>n2.val;
    }
};

struct node3{
    int u,v,w;
}e[MAXN];

void build(int u,int v,int w){
    edge[++k].to=v;
    edge[k].next=head[u];
    edge[k].val=w;
    head[u]=k;
}

void build2(int u,int v,int w){
    edge2[++k2].to=v;
    edge2[k2].next=head2[u];
    edge2[k2].val=w;
    head2[u]=k2;
}

void dij(int s,bool type){
    for(int i=1;i<=n;i++) vis[i]=false;
    for(int i=1;i<=n;i++) dis[type][i]=1e18;
    priority_queue<node2> q;
    dis[type][s]=0;
    q.push((node2){s,0});
    while(!q.empty()){
        int u=q.top().to;
        q.pop();
        if(vis[u]) continue;
        vis[u]=true;
        for(int i=head[u];i;i=edge[i].next){
            int v=edge[i].to;
            if(vis[v]) continue;
            if(dis[type][v]>dis[type][u]+edge[i].val){
                dis[type][v]=min(dis[type][v],dis[type][u]+edge[i].val);
                q.push((node2){v,dis[type][v]});
            }
        }
    }
}

void tarjan(int u,int fa){
    dfn[u]=low[u]=++times;
    for(int i=head2[u];i;i=edge2[i].next){
        //在最短路图上找割边，而不是在原图上找
        int v=edge2[i].to;
        if(v==fa) continue;
        if(dfn[v]==0){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v]){
                cut_edge[i]=true;
                cut_edge[i%2==0?i-1:i+1]=true;
                //反向边也要标记为割边
            }
        }
        else low[u]=min(low[u],low[v]);
    }
}

signed main(){
    read(n,m);
    for(int i=1;i<=m;i++){
        int u,v,w;
        read(u,v,w);
        e[i].u=u;e[i].v=v;e[i].w=w;
        build(u,v,w);
        build(v,u,w);
    }
    dij(1,false);
    dij(n,true);
    for(int i=1;i<=m;i++){
        int val1=dis[0][e[i].u]+dis[1][e[i].v]+e[i].w;
        int val2=dis[0][e[i].v]+dis[1][e[i].u]+e[i].w;
        if(val1==dis[0][n]||val2==dis[0][n]){
            y[i]=k2+1;
            build2(e[i].u,e[i].v,e[i].w);
            build2(e[i].v,e[i].u,e[i].w);
        }
    }
    for(int i=1;i<=n;i++) vis[i]=false;
    for(int i=1;i<=n;i++) if(dfn[i]==0) tarjan(i,0);
    for(int i=1;i<=m;i++){
        if(cut_edge[y[i]]) cout<<"Yes\n";
        else cout<<"No\n";
    }
    return 0;
}

LOADING

ABC375G 题解

题意简述

思路

实现

代码