是什么

Link-Cut-Tree 一般称作 LCT/虚实链剖分。
（ps： LCT 不能称作 动态树，动态树 指的是一类问题。）
由 Tarjan 发明（对，又是他），用于解决动态的树上路径/子树问题（统称为动态树问题）。
对于普通的树上问题，比如：

给定一颗 \(n\) 个节点的树，每个节点均有权值，需要维护三个操作：
1.查询 \(u\) 到 \(v\) 路径上的权值和
2.查询以 \(u\) 为根的子树的权值和
3.将 \(u\) 点的权值修改为 \(val\)

那么这是一道很板的树链剖分题。
但假如我们还需要维护两个操作：

4.将 \(u,v\) 这条边断开（如果有边的话）
5.将 \(u,v\) 连接起来（若 \(u,v\) 不在同一连通块内）

那么现在，普通的树剖就没有办法解决了。这时候，我们就需要用到 LCT。

怎么做

变量声明

\(root\) 表示树的根
\(tot\) 表示当前树的节点个数
\(val_{i}\) 表示 \(i\) 节点的权值
\(son_{i,0}\) 表示 \(i\) 节点的左儿子
\(son_{i,1}\) 表示 \(i\) 节点的右儿子
\(fa_{i}\) 表示 \(i\) 节点的父亲
\(tag_{i}\) 表示 \(i\) 节点的翻转标记
\(cnt_{i}\) 表示 \(i\) 节点存储的数量（同样的值放在同一个节点）
\(siz_{i}\) 表示以 \(i\) 节点为根的子树大小

先将 LCT 模板题放在 这里。
其实 LCT 的码量并不算太大，但是就比较难理解。

前置芝士：二叉搜索树，Splay。

二叉搜索树

我们在对一个序列进行各种操作的时候，可能会遇见让你插入某个数，删除某个数，还需要让你随时都保证有序，假如我们对一个普通的数组这样操作的话，如果从中间插入和删除之类的，需要用到 \(O(n)\) 的时间来维护序列的有序，这样的时间复杂度是无法接受的。于是我们将序列转移到一颗二叉树上。

输出

我们不妨让二叉树的中序遍历的结果，就是原先的序列。

那么怎么维护有序？假设我们需要维护单调递增的序列，对于每个节点 \(i\) 都满足 \(val_{son_{i,0}} < val_{i} < val_{son_{i,1}}\) 即可。

这样的话，经过中序遍历后得到的结果，就是单调递增的原序列了。

插入

设插入的值为 \(v\)。
根据前面所讲的输出方式，我们在插入的时候，使二叉树依然满足性质即可。
最开始令 \(pos \gets root\)。
（ps：\(a \gets b\) 表示将 \(b\) 的值赋给 \(a\)）
一直重复下面这个式子，直到 \(pos=0\)，或者 \(val_{pos}=v\)。

\[ \begin{cases} pos \gets son_{pos,0}(v<val_{pos})\\ pos \gets son_{pos,1}(v>val_{pos}) \end{cases} \]

找到插入的位置后，如果 \(pos=0\)，我们就可以将 \(tot \gets tot+1\) 并将新的这个权值 \(v\) 赋给 \(val_{tot}\)，再更新 \(fa_{tot}\) 和 \(son_{fa_{tot},0/1}\)。如果 \(pos\not =0\)，那我们只需要将 \(cnt_{pos} \gets cnt_{pos}+1\) 即可。
这样插入操作就完成了！
代码如下：

void insert(int v){
    int pos=root;
    int f=0;
    while(true){
        if(pos==0){
            val[++tot]=v;
            fa[tot]=f;
            if(f!=0) son[f][v>val[f]]=v;
            break;
        }
        fa=pos;
        if(v==val[pos]){
            cnt[pos]++;
            break;
        }
        pos=son[pos][v>val[pos]];
    }
}

查找某个值所在的位置

设需要查找的值为 \(v\)（保证 \(v\) 存在）。
那么就和插入操作很类似了，只是我们当 \(v=val_{pos}\) 的时候，直接返回 \(pos\) 即可
代码如下：

int selpos(int v){
    int pos=root;
    while(true){
        if(val[pos]==v) return pos;
        pos=son[pos][v>val[pos]];
    }
}

删除

设需要删除的值为 \(v\)。
删除操作需要先找到 \(v\) 的位置，删除后，合并他的左右两颗子树即可。
代码如下：

void clear(int pos){
    val[pos]=son[pos][0]=son[pos][1]=fa[pos]=0;
}//清空节点pos
void del(int v){
    int pos=selpos(v);
    if(son[pos][0]==0&&son[pos][1]==0){
        clear(pos);
        return;
    }
    if(son[pos][0]==0&&son[pos][1]!=0){
        fa[son[pos][1]]=fa[pos];
        if(fa[pos]!=0) son[fa[pos]][val[pos]>val[fa[pos]]]=son[pos][1];
        clear(pos);
        return;
    }
    if(son[pos][0]!=0&&son[pos][1]==0){
        fa[son[pos][0]]=fa[pos];
        if(fa[pos]!=0) son[fa[pos]][val[pos]>val[fa[pos]]]=son[pos][0];
        clear(pos);
        return;
    }
    fa[son[pos][0]]=son[pos][1];
    fa[son[pos][1]]=fa[pos];
    if(fa[pos]!=0) son[fa[pos]][val[pos]>val[fa[pos]]]=son[pos][1];
    clear(pos);
}

更多操作

• 查询 \(v\) 这个值的排名
  
• 查询 \(x\) 这个排名的值
  
• 查询 \(v\) 这个值的前驱
  
• 查询 \(v\) 这个值的后继

请读者自行尝试或者查阅，因为普通的二叉搜索树可以被很容易的卡成 \(O(n)\) 的，因此在后文讲解 Splay 时再具体讲解这些操作。

复杂度分析

空间复杂度：

我们每次在插入时只会多一个，因此空间复杂度为 \(O(n)\)。

时间复杂度：

理想情况下，\(n\) 个数据构成的二叉树的高度为 \(O(\log{n})\)，因此在插入删除时均最多跳 \(O(\log{n})\) 次，最优时间复杂度为 \(O(\log{n})\)。
但是我们可以通过构造如 1 2 3 4 5 这样单调的数据，来使树高变为 \(O(n)\)，此时二叉搜索树退化为链，插入和删除时最多会跳 \(n\) 次，最劣时间复杂度为 \(O(n)\)。

总之，普通的二叉搜索树没法保证时间复杂度，我们需要优化。

Splay

Splay 是一种自平衡的二叉搜索树。
（ps：关于更多平衡树，以后会讲）

Splay 通过一种叫做 Splay 的操作，防止二叉搜索树退化为链，保证了树高为 \(O(\log{n})\) 级别，保证了各个操作的 \(O(\log{n})\) 时间复杂度。

基础操作

直接上代码吧：

void clear(int x){
    fa[x]=val[x]=son[x][0]=son[x][1]=cnt[x]=siz[x]=0;
}//清空x节点
void pushup(int x){
    siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x];
}//更新x节点的子树大小
bool get(int x){
    return x==son[fa[x]][1];
}//得到点x属于fa[x]的左儿子还是右儿子

旋转操作

若你学过 Treap 之类的带旋平衡树，这一部分可以选择略过。

由中序遍历的性质：同一种中序遍历对应的二叉树不止一棵。
我们可以通过一些操作，在保证中序遍历不变的前提下，来使树高变低。
这种操作就称作 旋转操作，函数一般叫做 rotate。

为什么要旋转

对于这么一棵二叉树。

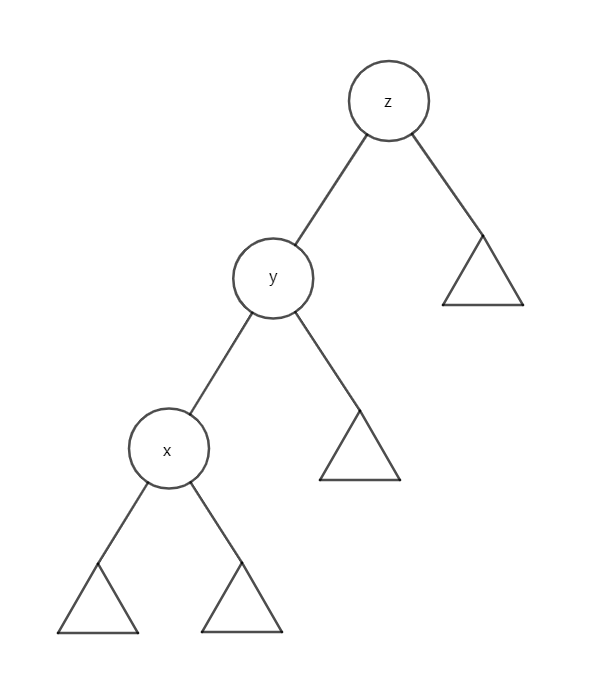
我们要将其转成这样：

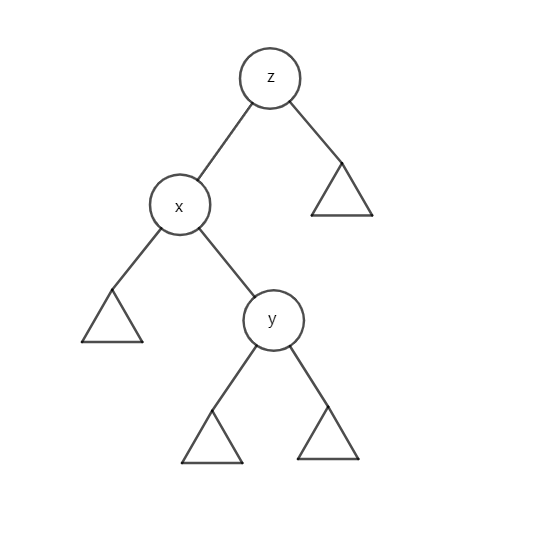
当然也可以转回来。
这样进行一次旋转后，x的高度提高了一层，看似对总的高度没有影响，但对于这样的退化成链的情况时：

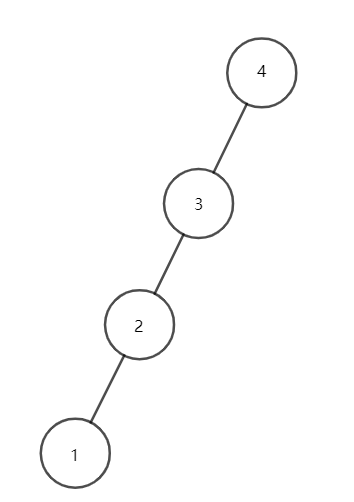
我们可以通过如下操作，将高度降低。

1. 对点 \(1\) 进行旋转操作，会变成这样：

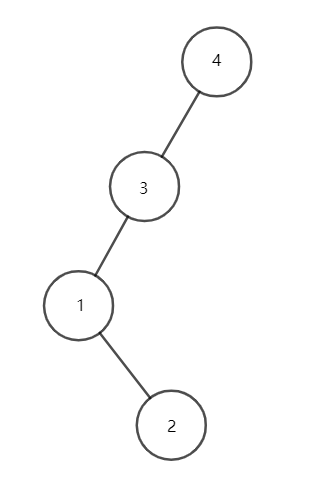
2. 再对点 \(1\) 进行旋转操作，会变成这样：

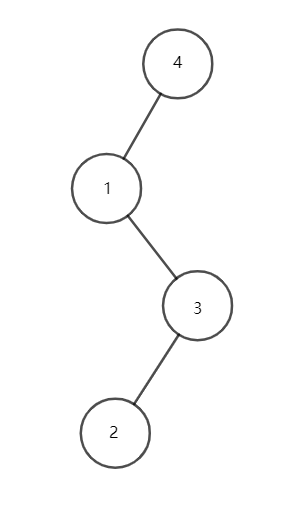
3. 继续对点 \(1\) 进行旋转操作，会变成这样：

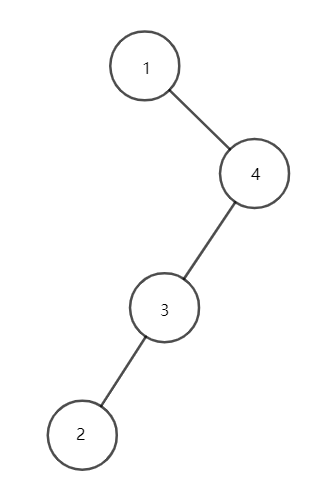
4. 最后对点 \(3\) 进行旋转操作，会变成这样：

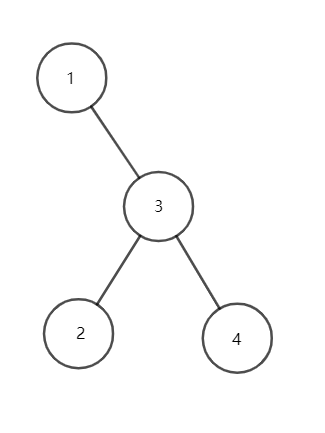
至此，我们成功地通过旋转操作将高度从 \(4\) 降到 \(3\)。
因此旋转操作是可以有效降低树高的。

旋转过程讲解

我们令要进行 rotate 操作的点为 \(x\)。
令:
\(y \gets fa_{x}\)
\(z \gets fa_{y}\)
\(ch \gets get(x)\)

根据这两个图：

我们可以发现：
（ps：\(a \oplus b\) 表示 "\(a\) 异或 \(b\)"）
（此时的 \(ch=0\)）

• \(son_{x,ch}\) 没有发生变化
  
• \(son_{x,ch \oplus 1}\) 变成了 \(y\)
  
• \(son_{y,ch}\) 从 \(x\) 变成了 \(son_{x,ch \oplus 1}\)
  
• 对应的 \(fa\) 的的值也会随之变化

最后再处理一下先后执行顺序，就可以写出旋转操作的代码啦~~

代码

void rotate(int x){
    int y=fa[x],z=fa[y];bool ch=get(x);
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]!=0) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    fa[y]=x;
    fa[x]=z;
    if(z!=0) son[z][y==son[z][1]]=x;
    pushup(y);
    pushup(x);
}

Splay操作

Splay 规定，每次操作后，都要将操作的点转到根上，这样的操作就被称为 Splay操作。
怎么转移到根上？暴力一次次往上旋转即可。

单旋Splay

如果只是像上文那样旋转，也就是从下往上依次转，这样的被称为 单旋Splay。
当出现 \(x,y,z\) 三点共线时，我们发现，依此转完后，树高是没有变化的，这样就没法保证时间复杂度（见下面几张图理解）。

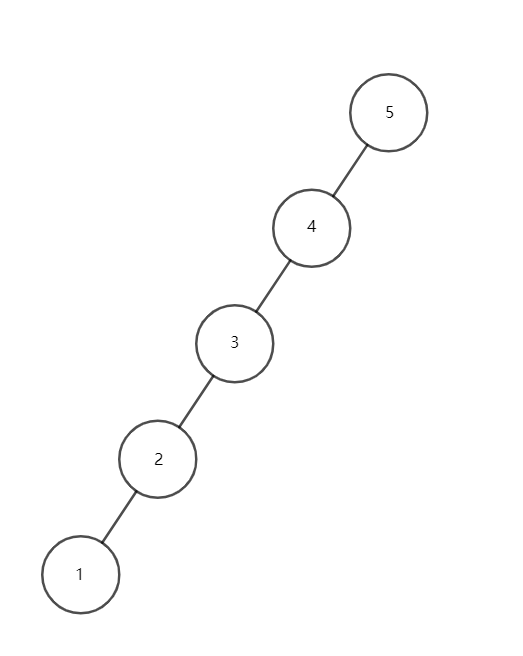
我们需要将 \(1\) 号点转到根上。

那么我们只需要旋转四次 \(1\) 号点就可以了。
转的过程如下：

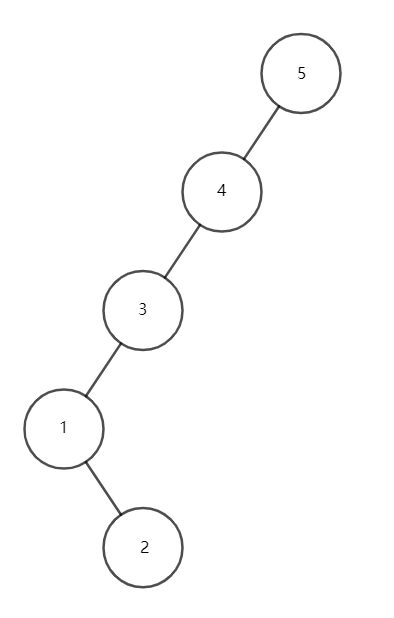
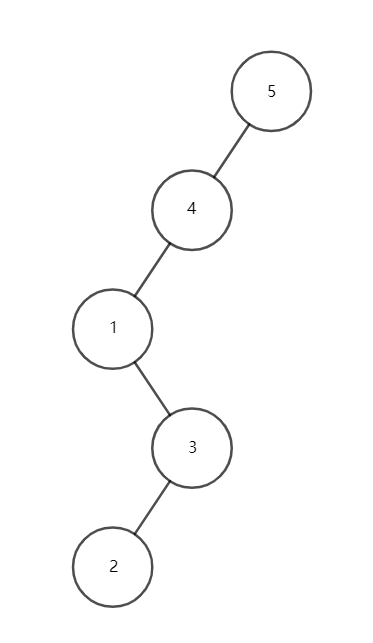
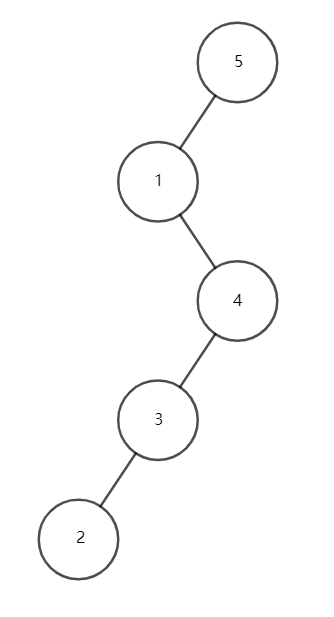
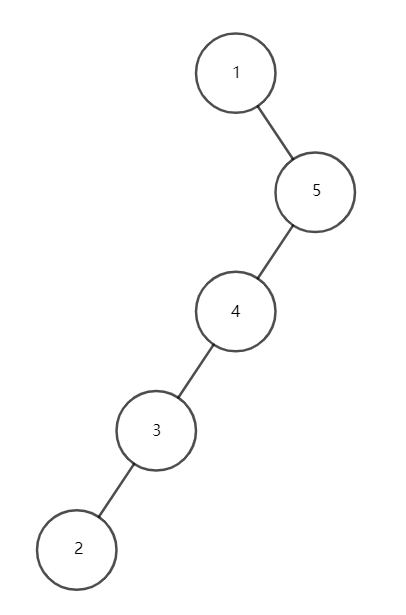
这样的话，就是“如转”，我们虽然将 \(1\) 号点转到了根上，但是高度并没有降低。
因此当树退化为一条链的时候，单旋Splay 也就没法保证时间复杂度了。

这时候我们就需要用到 双旋Splay。

双旋Splay

双旋Splay 其实就是在 单旋Splay 的基础上，特殊处理了一下 \(u,v,z\) 三点共线的情况。
在遇到三点共线的情况时，我们只需要先旋转 \(fa_{u}\) 也就是 \(v\) 点，再旋转 \(u\) 点即可。
因为我们在旋转某个点的时候，这个点的整个子树都会一起上升 \(1\) 层。
因此我们先转 \(v\)，后转 \(u\) 是合法的。
（见下图模拟，我们依然需要将 \(1\) 号点转到根上）

\(1,2,3\) 号点共线，因此先转 \(2\) 号点，再转 \(1\) 号点。

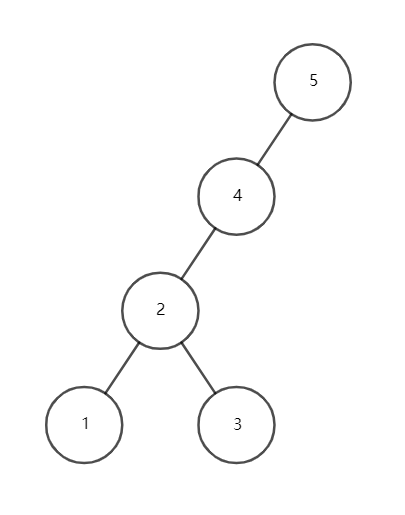
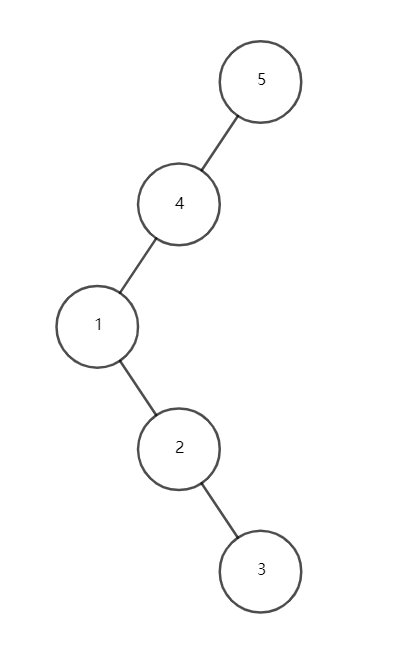
\(1,4,5\) 号点共线，因此先转 \(4\) 号点，再转 \(1\) 号点。

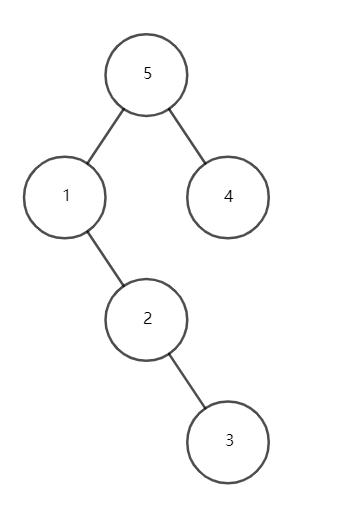
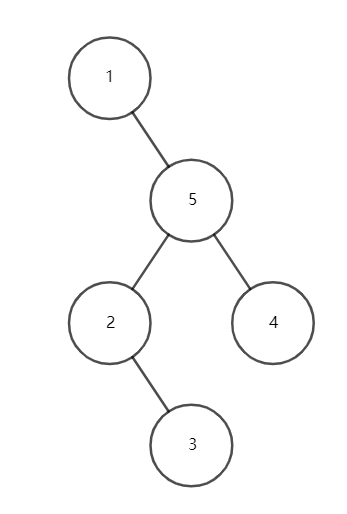
可见，双旋Splay 不仅将我们需要的点转到了根上，而且将原来的不优美的链，变得优美了一些些，高度也就降低了，因此 双旋Splay 更优。

//这里的to表示要转到哪个点去，一般是转到根，也就是to==root
void Splay(int x,int &to){
    int z=fa[to];
    for(int f=fa[x];f!=z;f=fa[x]){
        if(fa[f]!=z) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
    to=x;
}

现在我们学会了 Splay操作，那么其实也就很简单了，只需要像普通的二叉搜索树一样进行操作基本就行了，记住每次操作完后，将最后找到的点通过 Splay操作 转到根上去就可以了。

插入

因为 Splay 本质上也是二叉搜索树，因此它满足二叉搜索树有的所有性质。
插入方式和普通二叉搜索树一样，记住最后将插入的那个点旋转到根上即可~

代码如下：

void insert(int x){
    if(root==0){
        val[++tot]=x;
        cnt[tot]++;
        pushup(tot);
        root=tot;
        return;
    }
    int f=0,pos=root;
    while(true){
        if(val[pos]==x){
            cnt[pos]++;
            pushup(pos);
            pushup(f);
            Splay(pos,root);//记住Splay操作！！！
            return;
        }
        f=pos;
        pos=son[pos][x>val[pos]];
        if(pos==0){
            val[++tot]=x;
            cnt[tot]++;
            fa[tot]=f;
            son[f][x>val[f]]=tot;
            pushup(tot);
            pushup(f);
            Splay(tot,root);//记住Splay操作！！！
            return;
        }
    }
}

查询排名

设当前访问到的点是 \(pos\)，答案为 \(ans\)，最开始 \(ans \gets 1\)（因为排名至少为 \(1\)）。
查询 \(x\) 这个值的排名可以分为三种情况：

1. \(x > val_{pos}\)：
   说明 \(pos\) 这个点的左子树的所有值和 \(pos\) 这个点的值都小于 \(x\)
   那么排名至少为 \(cnt_{son_{pos,0}}+cnt_{pos}\)
   即 \(ans \gets ans+cnt_{son_{pos,0}}+cnt_{pos}\)
   然后继续到右子树中计算答案，即 \(pos \gets son_{pos,1}\)
   
2. \(x = val_{pos}\)：
   说明 \(pos\) 的左子树的所有值都小于 \(x\)
   并且 \(pos\) 这个点的值刚好等于 \(x\)
   因此排名就应该是 \(ans \gets ans+siz_{son_{pos,0}}\)
   
3. \(x < val_{pos}\)：
   说明 \(pos\) 的左子树有比 \(x\) 大的值。
   因此此时不能对答案进行计算。
   需要继续到左子树中计算答案，即 \(pos \gets son_{pos,1}\)

int selrank(int x){
    int res=0,pos=root;
    while(true){
        if(x==val[pos]){
            Splay(pos,root);//将pos转到根后，其左子树就是答案，其实和前文表述是一样的
            return siz[pos[son][0]]+1;
        }
        if(pos==0) break;
        if(x<val[pos]) pos=son[pos][0];
        else{
            res+=siz[son[pos][0]]+cnt[pos];
            pos=son[pos][1];
        }
    }
    return res+1;   
}

查询排名对应的值

查询排名对应的值其实和查询值对应的排名很像。
设当前访问到的点是 \(pos\)，要找排名为 \(x\) 的值。
一样分为3种情况：

1. \(x > siz_{son_{pos,0}}+cnt_{pos}\)：
   说明答案在 \(pos\) 的右子树中。
   因此将 \(x \gets x-(siz_{son_{pos,0}}+cnt_{pos})\)
   再到右子树（\(pos \gets son_{pos,1}\)）中寻找答案即可。
   
2. \(siz_{son_{pos,0}} < x \le siz_{son_{pos,0}}+cnt_{pos}\)：
   说明答案就是 \(val_{pos}\)
   直接返回答案即可。
   
3. \(x \le siz_{son_{pos,0}}\)：
   说明答案在 \(pos\) 的左子树。
   到左子树（\(pos \gets son_{pos,0}\)）中继续寻找答案即可。

//rt表示要在以哪个点为根的子树里寻找
int selval(int x,int &rt){
    int pos=rt;
    while(true){
        if(x<=siz[son[pos][0]]&&son[pos][0]){
            pos=son[pos][0];
            continue;
        }
        x-=siz[son[pos][0]]+cnt[pos];
        if(x<=0){
            Splay(pos,rt);//记住Splay操作！！！
            return val[pos];
        }
        pos=son[pos][1];
    }
}

查询前驱

前驱被定义为比 \(x\) 小的数中最大的数。
因此我们只需要先将 \(x\) 转到根上，再从根的左子树开始，一直跳右儿子即可。

int selpre(){
    int pos=son[root][0];
    while(son[pos][1]!=0) pos=son[pos][1];
    Splay(pos,root);//记住Splay操作！！！
    return pos;
}

注意：这个是找的是当前根所对应的值的前驱，如果需要查找任意一个数的前驱，可以先插入这个数，查完后再删除即可。

int selpre_val(int x){
    int res;
    insert(x);
    res=val[selpre()];
    del(x);
    return res;
}

查询后继

查找后继和前驱基本一致，只是开始从根的左儿子变成了右儿子，跳左儿子变成了跳右儿子。

int selnext(){
    int pos=son[root][1];
    while(son[pos][0]!=0) pos=son[pos][0];
    Splay(pos,root);//记住Splay操作！！！
    return pos;
}

查找任意一个数的后继和查找任意一个数的前驱是同样的道理：

int selpre_val(int x){
    int res;
    insert(x);
    res=val[selnext()];
    del(x);
    return res;
}

合并两颗Splay树

两颗 Splay树 想要快速合并，前提条件是一棵树的最大值小于另一棵树的最小值，否则无法做到快速合并。

合并分为三种情况:

1. 两棵子树均为空，不用管。
   
2. 一棵子树为空，直接把不为空的子树的根作为合并后的根即可。
   
3. 两边子树均不为空，将第一棵子树的最大值转到根上，将左儿子设为另一颗树的根，\(fa\) 数组也跟着更新即可，最后合并出的根就是第一棵子树的根。

为什么要将一棵树的最大值转到根后再合并？因为这样才能保证第一棵子树的右儿子是空的，才能够合并上去。

int merge(int x,int y){//这里传的是两个树的根，返回值是合并后的根
    if(x==0||y==0) return x+y;
    int pos=x;
    while(son[pos][1]!=0) pos=son[pos][1];
    Splay(pos,root);//记住Splay操作！！！
    son[pos][1]=y;
    fa[y]=pos;
    pushup(pos);
    return pos;
}

删除

删除操作相对比较复杂。
因此放在最后面来讲 需要先将要删的这个点转到根上。
如果这个点的 \(cnt\) 值大于 \(1\)，那么直接将 \(cnt_{pos} \gets cnt_{pos}-1\) 即可。 然后再找到这个点的前驱。
将前驱作为新的根，合并两颗子树。

为什么要找前驱？
因为在当前你要删除的这个点的右子树中，只有前驱可以保证没有右儿子。
合并两棵子树也就是 \(O(1)\) 的了。

void del(int x){
    selrank(x);//这里的作用是将x转到根上
    if(cnt[root]>1){
        cnt[root]--;
        pushup(root);
        return;
    }
    if(son[root][0]==0&&son[root][1]==0){
        clear(root);
        root=0;
        return;
    }
    if(son[root][0]==0&&son[root][1]!=0){
        int past=root;
        root=son[root][1];
        fa[root]=0;
        clear(past);
        return;
    }
    if(son[root][0]!=0&&son[root][1]==0){
        int past=root;
        root=son[root][0];
        fa[root]=0;
        clear(past);
        return;
    }
    int past=root;
    int pos=selpre();//此时的pos已经成为根了，所以不用Splay操作了
    fa[son[past][1]]=pos;
    son[pos][1]=son[past][1];
    clear(past);
    pushup(root);
}

代码

至此，你已经会了 Splay 的绝大多数操作了
板子的代码也放在这里了~

ps：亲测本人 Splay 代码可以通过加强版模板题

代码如下：

// Problem: P3369 【模板】普通平衡树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3369
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
const int mod1=1e9+7;
const int mod2=998244353;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

int n,tot,root,cnt[MAXN],val[MAXN],fa[MAXN],son[MAXN][2],siz[MAXN];

int get(int x){return x==son[fa[x]][1];}
void pushup(int x){siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x];}
void clear(int x){siz[x]=cnt[x]=val[x]=fa[x]=son[x][0]=son[x][1]=0;}

void rotate(int x){
    int y=fa[x],z=fa[y],ch=get(x);
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    if(z) son[z][get(y)]=x;
    fa[y]=x;fa[x]=z;
    pushup(y);pushup(x);
}

void Splay(int x,int &rt){
    int z=fa[rt];
    for(int f=fa[x];f!=z;f=fa[x]){
        if(fa[f]!=z) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
    rt=x;
}

void insert(int x){
    if(root==0){
        cnt[++tot]=1;
        siz[tot]=1;
        val[tot]=x;
        root=tot;
        return;
    }
    int f=0,pos=root;
    while(true){
        if(val[pos]==x){
            cnt[pos]++;
            pushup(pos);
            pushup(f);
            Splay(pos,root);
            return;
        }
        f=pos;
        pos=son[pos][x>val[pos]];
        if(pos==0){
            cnt[++tot]++;
            val[tot]=x;
            fa[tot]=f;
            son[f][x>val[f]]=tot;
            pushup(tot);
            pushup(f);
            Splay(tot,root);
            return;
        }
    }
}

int selrank(int x){
    int res=0,pos=root;
    while(true){
        if(val[pos]==x){
            Splay(pos,root);
            return siz[son[pos][0]]+1;
        }
        if(pos==0) break;
        if(val[pos]<x){
            res+=siz[son[pos][0]]+cnt[pos];
            pos=son[pos][1];
        }
        else pos=son[pos][0];
    }
    return res+1;
}

int selval(int x,int &rt){
    int pos=rt;
    while(true){
        if(x<=siz[son[pos][0]]&&son[pos][0]){
            pos=son[pos][0];
            continue;
        }
        x-=siz[son[pos][0]]+cnt[pos];
        if(x<=0){
            Splay(pos,rt);
            return val[pos];
        }
        pos=son[pos][1];
    }
}

int selpre(){
    int pos=son[root][0];
    while(son[pos][1]) pos=son[pos][1];
    Splay(pos,root);
    return pos;
}

int selnext(){
    int pos=son[root][1];
    while(son[pos][0]) pos=son[pos][0];
    Splay(pos,root);
    return pos;
}

void del(int x){
    selrank(x);
    if(cnt[root]>1){
        cnt[root]--;
        pushup(root);
        return;
    }
    if(son[root][0]==0&&son[root][1]==0){
        clear(root);
        root=0;
        return;
    }
    if(son[root][0]!=0&&son[root][1]==0){
        int past=root;
        root=son[root][0];
        fa[root]=0;
        clear(past);
        return;
    }
    if(son[root][0]==0&&son[root][1]!=0){
        int past=root;
        root=son[root][1];
        fa[root]=0;
        clear(past);
        return;
    }
    int past=root;
    int pos=selpre();
    fa[son[past][1]]=pos;
    son[pos][1]=son[past][1];
    clear(past);
    pushup(root);
}

signed main(){
    read(n);
    for(int i=1;i<=n;i++){
        int opt,z;
        read(opt,z);
        if(opt==1) insert(z);
        if(opt==2) del(z);
        if(opt==3) cout<<selrank(z)<<'\n';
        if(opt==4) cout<<selval(z,root)<<'\n';
        if(opt==5){insert(z);cout<<val[selpre()]<<'\n';del(z);}
        if(opt==6){insert(z);cout<<val[selnext()]<<'\n';del(z);}
    }
    return 0;
}

还没结束！

在平衡树的相关模板中，除了【模板】普通平衡树，【模板】普通平衡树（数据加强版）外，还有一道【模板】文艺平衡树。（当然还有【模板】可持久化平衡树和【模板】可持久化文艺平衡树，但这个是 FHQ 干的事，我还不会。似乎还有一个神秘的【模板】后缀平衡树）

文艺平衡树

所谓文艺平衡树，其实是让你支持一种操作，区间翻转。
这个操作看起来不太可做，实际上，我们可以利用二叉搜索树的性质来实现。

我们知道，二叉搜索树的中序遍历也就是原序列。
我们为了实现区间翻转的操作，我们不妨修改一下，我们改成：

中序遍历是原序列从左到右的遍历结果。

那么我们又可以得到这些性质：

• Splay 上每一个元素代表了原序列的每一个元素。
  
• Splay 上的每一棵子树都代表了原序列中一段的数。

那么，在初始建树的时候，我们只需要按照序列原先的顺序，挨个挨个建一条只有左儿子的链就行了。

void build(int n){
    for(int i=1;i<=n+2;i++){
        son[++tot][0]=root;
        if(root!=0) fa[root]=tot;
        root=tot;
        val[tot]=i-1;
    }
    Splay(1,root);//从下往上更新一下节点信息
}

那么我们怎么翻转呢？
显然我们只需要将一棵子树的左右儿子挨个挨个调换位置就可以了。
但如果我们直接每次翻转都去做一遍的话，时间复杂度显然会是 \(O(n)\) 的。我们考虑像线段树一样，记录一个 lazy 标签，需要下传的时候，再下传标记就可以了。

void rev(int u){
    swap(son[u][0],son[u][1]);
    tag[u]^=1;
}

void pushdown(int x){
    if(tag[x]){
        if(son[x][0]) rev(son[x][0]);
        if(son[x][1]) rev(son[x][1]);
        tag[x]=0;
    }
}

那我们怎么对区间 \([L,R]\) 进行翻转呢？我们每次翻转是翻转一整棵子树，而一棵子树，又恰好对应了原序列的一段区间，因此我们只需要尝试将 \([L,R]\) 区间弄到同一棵子树内就可以了。

根据中序遍历，一个结点的右子树对应的编号一定是比这个点对应的编号要大的。而左子树都是要更小的。
所以我们不妨先把 \(L-1\) 转到根上，再将 \(R+1\) 转到 \(L-1\) 的右子树的根上。这样，\(R+1\) 的左子树对应的区间便是 \([L,R]\) 了。因为 \(L\) 可能为 \(1\)，\(R\) 可能为 \(n\)，此时 \(L-1=0,R+1=n+1\) 所以我们在初始建树的时候，便可以先在一前一后加上两个空节点。
然后翻转的时候打个 lazy 标签，往下走的时候下传标签就好了。
一定要记住，往下走的时候，就要下传一次标签！！！

void reverse(int l,int r){
    selval(l,root);//因为初始序列前后各加了一个数，所以这里找第l个，刚好就是原序列的第l-1个
    selval((r+1)-(l-1),son[root][1]);
    int now=son[son[root[1]]][0];
    rev(now);
    pushdown(now);
    Splay(now,root);
}

其他部分和普通的平衡树差不多。

// Problem: P3391 【模板】文艺平衡树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3391
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
const int mod1=1e9+7;
const int mod2=998244353;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

int n,m,tot,root,val[MAXN],siz[MAXN],tag[MAXN],fa[MAXN],son[MAXN][2],cnt[MAXN];

int get(int x){return x==son[fa[x]][1];}
void pushup(int x){siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x];}
void rev(int x){swap(son[x][0],son[x][1]);tag[x]^=1;}

void rotate(int x){
    int y=fa[x],z=fa[y],ch=get(x);
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    if(z) son[z][get(y)]=x;
    fa[x]=z;fa[y]=x;
    pushup(y);pushup(x);
}

void Splay(int x,int &rt){
    int z=fa[rt];
    for(int f=fa[x];f!=z;f=fa[x]){
        if(fa[f]!=z) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
    rt=x;
}

void build(int n){
    for(int i=0;i<=n+1;i++){
        son[++tot][0]=root;
        if(root) fa[root]=tot;
        root=tot;
        val[tot]=i;
        cnt[tot]++;
    }
    Splay(1,root);
}

void pushdown(int x){
    if(tag[x]){
        if(son[x][0]) rev(son[x][0]);
        if(son[x][1]) rev(son[x][1]);
        tag[x]=0;
    }
}

int selval(int x,int &rt){
    int pos=rt;
    while(true){
        pushdown(pos);
        if(x<=siz[son[pos][0]]&&son[pos][0]) pos=son[pos][0];
        else{
            x-=siz[son[pos][0]]+cnt[pos];
            if(x<=0){
                Splay(pos,rt);
                return val[pos];
            }
            pos=son[pos][1];
        }
    }
}

void reverse(int l,int r){
    selval(l,root);
    selval((r+1)-(l-1),son[root][1]);
    int x=son[son[root][1]][0];
    rev(x);
    pushdown(x);
    Splay(x,root);
}

void print(int x){
    if(!x) return;
    pushdown(x);
    print(son[x][0]);
    if(val[x]>=1&&val[x]<=n) cout<<val[x]<<" ";
    print(son[x][1]);
}

signed main(){
    read(n,m);
    build(n);
    for(int i=1;i<=m;i++){
        int l,r;
        read(l,r);
        reverse(l,r);
    }
    print(root);
    return 0;
}

好，文艺平衡树到这里也就结束了！
接下来，就正式进入 LCT 的部分了~

LCT

现在，你应该已经掌握了所有的前置芝士，是时候真正进入LCT的部分了！！！

讲解

首先，我们称原来的树叫做原树。
现在，我们为了实现删边和连边的操作，引入一棵新的树，叫做辅助树。
注意！！！千万千万不要把这两棵弄混了！！！
在下文中，我会将有关这两棵树的地方用不同的颜色标出。
这是\(\textcolor{green}{原树}\)，这是\(\textcolor{blue}{辅助树}\)。

既然 LCT 又叫做虚实链剖分，那么肯定和一般的树剖有相似之处。
我们定义有两种树边，一种是实边，一种是虚边，对应的连接的儿子也就分别是实儿子和虚儿子。
\(\textcolor{green}{原树}\)中有儿子的节点一定有且仅有一条实边（没有儿子当然也就没有实边），可以有任意多（包括 \(0\)）条虚边。
虚实链都是可以自由变换的，这个特点使得 LCT 可以实现 动态树 这一类问题。
将由实边构成的树上的一条链称为实链。显然，每个点都会且仅会在一条实链上。

\(\textcolor{green}{原树}\)上的每一条实链，在\(\textcolor{blue}{辅助树}\)上对应的则是一棵 Splay。

\(\textcolor{blue}{辅助树}\)有如下性质：

1. \(\textcolor{blue}{辅助树}\)上每个点与\(\textcolor{green}{原树}\)上的每个点一一对应。
   
2. 对\(\textcolor{blue}{辅助树}\)上每一棵 Splay 树进行中序遍历，得到的则是\(\textcolor{green}{原树}\)上这条对应的实链从上到下的路径。
   
3. \(\textcolor{blue}{辅助树}\)上每一棵 Splay 树的根节点是有父亲的。定义为\(\textcolor{blue}{辅助树}\)上这棵 Splay 对应的\(\textcolor{green}{原树}\)上的那条实链的最顶端的节点的父亲。（特别的，最顶端的 Splay 的根节点是没有父亲节点的，或者说它的父亲节点是 \(0\)）
   
4. 在 \(3\) 中提到的父亲关系的特点是儿子认父亲，父亲不认儿子。而\(\textcolor{blue}{辅助树}\)上的每一棵 Splay 内部的父亲关系则是儿子认父亲，父亲认儿子的。
   
5. 在 LCT 上的所有操作，都只需要在\(\textcolor{blue}{辅助树}\)上操作即可，因为每一棵\(\textcolor{blue}{辅助树}\)都会对应唯一的一棵\(\textcolor{green}{原树}\)。

假如我们有这样一棵\(\textcolor{green}{原树}\)：

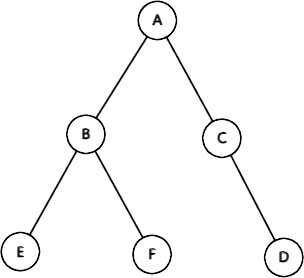
他的虚实链剖分可能长这样（因为虚实链很自由的原因，所以这并不是唯一一种剖分方式）：

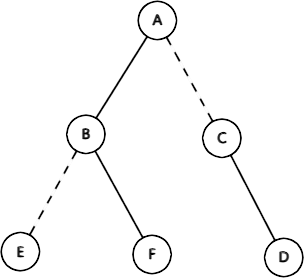
虚线边表示虚边，实线边表示实边。

那么根据定义，这棵\(\textcolor{green}{原树}\)对应的\(\textcolor{blue}{辅助树}\)可能就会是这样的：

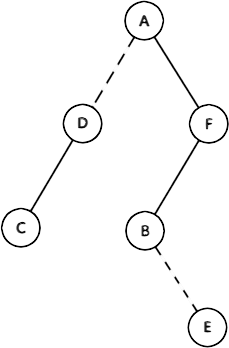
那么我们现在就需要思考，\(\textcolor{blue}{辅助树}\)是如何实现 动态树 这么一个难题的呢？

既然叫做 Link-Cut Tree，那么肯定就要 Link 和 Cut，下面我们来看看怎么连边。

如何连边

拿这么两棵树举例：

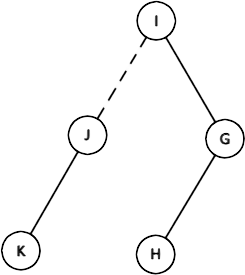
我们需要把 \(G\) 和 \(B\) 连接起来，那么树就变成这个样子：

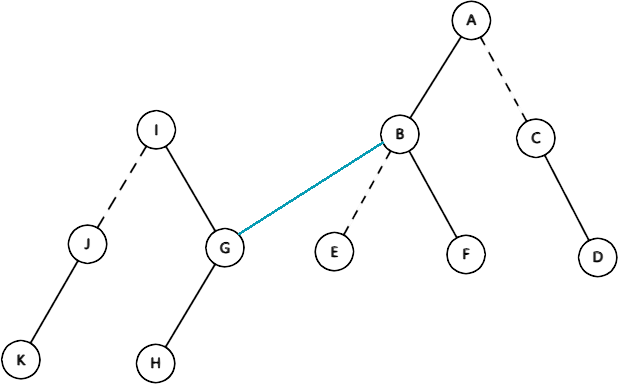
我们发现蓝色边无论是实边，还是虚边，都是无法建出一棵合法的\(\textcolor{blue}{辅助树}\)的。因此我们要么在\(\textcolor{green}{原树}\)上作出修改，要么在\(\textcolor{blue}{辅助树}\)上做修改。
根据前文所讲，我们只需要，也只能在\(\textcolor{blue}{辅助树}\)上做修改。
那么我们怎么修改呢？

原先两棵树的\(\textcolor{blue}{辅助树}\)可以是这样的：

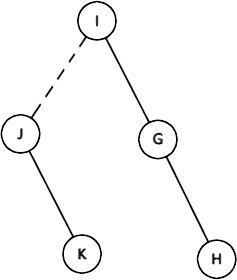
那么假如直接连接 \(G\) 和 \(B\) 就会是这样的：

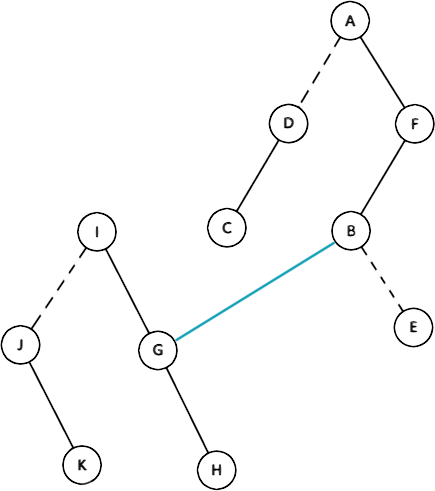
很显然的发现，这样是不合法的，因为 \(G\) 有了两个父亲。
根据\(\textcolor{blue}{辅助树}\)的性质 \(3\)，我们知道，只有整棵\(\textcolor{blue}{辅助树}\)的根节点才是没有父亲的。
因此我们需要把 \(G\) 点变成它所在的\(\textcolor{blue}{辅助树}\)的根的位置。
我们定义一种新的函数叫做 access(x)，表示将 x 这个点与其当前变所在的\(\textcolor{green}{原树}\)的根结点弄到同一个 Splay 中。也就是将 x 到根的路径变成一条实链。
那么在这个例子中，我们进行一次 access(G)，再 Splay(G) 一下，最后，连接 \(G\) 和 \(B\)，似乎就达成了任务，此时变为：

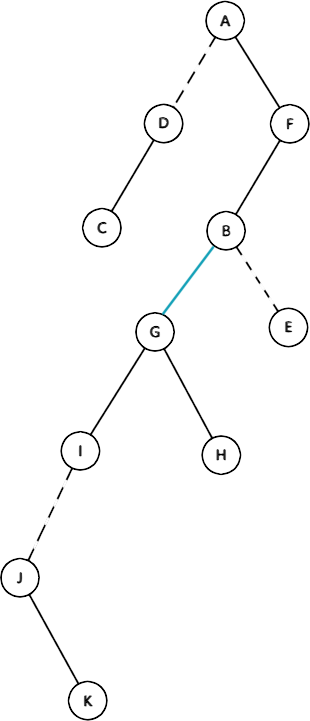
但从\(\textcolor{green}{原树}\)的连接情况中我们可以看出：

根据\(\textcolor{blue}{辅助树}\)的性质 \(2\)，在这棵\(\textcolor{blue}{辅助树}\)上，\(I,G,H\) 应该深度依次递增。但我们发现在连接后的\(\textcolor{green}{原树}\)上（假设以 \(A\) 点为根）并不满足这一点，因此目前的连接情况是不合法的。
怎么处理这种情况？
那么很显然的，我们让 \(G\) 这个点变成它所在的\(\textcolor{green}{原树}\)的根就可以了。
我们称这样将某个点变成其所在的\(\textcolor{green}{原树}\)的根的操作为 makeroot(x)，当然，我们依然只能在\(\textcolor{blue}{辅助树}\)上进行一些操作。
那么这个 makeroot(x) 函数以及前文中的 access(x) 函数分别该怎样实现呢？

access

这里再用上文中的\(\textcolor{green}{原树}\)的例子就不大好了。我们换一棵\(\textcolor{green}{原树}\)：

（这里就直接搬了 OI-Wiki 上的原图了xwx）

（这里以 \(A\) 点为\(\textcolor{green}{原树}\)的根。）
这棵\(\textcolor{green}{原树}\)的\(\textcolor{blue}{辅助树}\)可能长这样：

假如我们想要 access(N)。

也就是将\(\textcolor{green}{原树}\)变为这样：

（红色的边表示的是有虚实边类型切换的边）

首先我们肯定需要先将 \(N\) 转到其所在的 Splay 的根处，这样我们才能继续往上嘛。
根据 access 的定义，我们需要将原来 \(N\) 到 \(O\) 的实边变为虚边。
根据\(\textcolor{blue}{辅助树}\)认父不认子的特点，我们可以直接将 \(N\) 的儿子变成不存在。
那么\(\textcolor{blue}{辅助树}\)就变成了这样：

然后，我们需要把 \(N\) 与其在\(\textcolor{blue}{辅助树}\)上的父亲 \(I\) 打通。根据前面所讲，\(I\) 点也就是 \(N\) 目前所在的实链的顶端的点的父亲。
那么我们要将 \(N\) 与 \(I\) 打通，肯定需要先将 \(I\) 原来的实儿子取消掉。这个我们只需要先将 \(I\) 点转到其所在的 Splay 的根处，然后 \(I\) 原来的实儿子一定位于其在 Splay 上的右儿子处，直接将 \(rson_{I}\) 变成不存在就行了。
然后，我们将 \(N\) 设置为 \(I\) 的右儿子即可。
那么\(\textcolor{blue}{辅助树}\)也就变成了这样：

重复上述操作，直到 \(A\) 和 \(N\) 在同一棵 Splay 中。

那么 access(N) 的任务就完成啦！

总结一下，access 操作也就是以下几步：

1. 将当前点转到根上
   
2. 将当前点的右儿子换成上一个点
   
3. 更新一下当前点的信息
   
4. 将当前点换成当前点的父亲

代码如下：

int access(int x){
    int now=0;
    for(;x;now=x,x=fa[x]) Splay(x),son[x][1]=now,pushup(x);
    pushup(x);
    return now;
}

注意到这里的 access 函数有一个返回值。
这个返回值代表的是：最后一次进行虚实边变换的时候，虚边的父亲对应的编号。就比如在上面的例子中，最后一次变换的是 \(A\) 到 \(B\) 这条边，这两条边的父亲节点都是 \(A\)，所以最后会返回 \(A\)。
这个东西有什么用呢？我们后面再说。

makeroot

makeroot 的重要性不亚于 access，在前文我们已经讲解了为什么要使用 makeroot，以及 makeroot 的作用。现在我们直接来讲怎么做。

假设我们现在有这么一棵\(\textcolor{green}{原树}\)：

虽然我们的\(\textcolor{green}{原树}\)是无向的，但是我们不妨假设其有向。（假设以 \(1\) 号点为根）

那我们发现，我们假如要让 \(4\) 号点变成\(\textcolor{green}{原树}\)的根，我们需要把树变成这样：

我们发现，其实也就是将 \(1\) 号点到 \(4\) 号点的路径进行了翻转。
那么也就是说，我们想要将某个点变成\(\textcolor{green}{原树}\)的根，我们只需要将其到根节点的路径进行翻转就可以了。
这个操作和 Splay 的翻转操作是类似的。

代码：

void makeroot(int x){
    x=access(x);Splay(x);
    swap(son[x][0],son[x][1]);
    tag[x]^=1;
}

这里的 access 函数，将 \(u\) 和当前的根放在了同一 Splay 下。但是我们又令 \(u\gets \operatorname{access}(u)\)，这是为什么呢？
我们前面在学习 Splay 的翻转操作时知道，Splay 的翻转操作是需要对一整棵子树操作的，而这里 access(u) 返回的值，恰好就是这棵 Splay 的根，为什么？看看 access 的代码，就明白了。

那我们现在，makeroot 函数也搞定了，终于可以连边了~直接按照前文所说的来操作就行了，注意先判一下要连的边是否在同一棵树中，如果在同一棵树中显然是不能连边的。

void link(int x,int y){
    makeroot(x);Splay(x);
    if(findroot(y)!=x) fa[x]=y;
}

如何删边

Link-Cut 中的 Link 我们解决了，那 Cut 呢？

我们现在要删掉 \(x\) 与 \(y\) 之间的边，显然，我们需要判断这个操作是否合法，也就是 \(x\) 与 \(y\) 当前有没有边。这怎么去判断呢？
当然你可以选择用 map 来存一下边。

首先，要有边，\(x\) 与 \(y\) 必须得是联通的。也就是 \(x\) 和 \(y\) 在同一棵树内。\(\textcolor{blue}{辅助树}\)的根会经常变化，而\(\textcolor{green}{原树}\)的根只有在调用 makeroot 函数的时候才会发生变化，因此我们要知道 \(x\) 和 \(y\) 是否在同一棵子树中，只需要判断 \(x\) 与 \(y\) 所在的\(\textcolor{green}{原树}\)的根是否是同一个点就行了。

怎么去找一个点所在\(\textcolor{green}{原树}\)的根呢？我们稍后再讲。我们现在先把判断合法的条件讲完。

\(x\) 与 \(y\) 在同一棵树中显然并不能说明他们俩之间有边。而且我们只知道\(\textcolor{blue}{辅助树}\)的形态。我们不妨先 makeroot(x)，这样的话，\(y\) 的就一定深于 \(x\) 了。我们令这个函数叫做 findroot。
我们知道，LCT 将\(\textcolor{green}{原树}\)拆成了若干条链，那么如果 \(x\) 与 \(y\) 在同一条实链上，至少可以说明它俩在\(\textcolor{green}{原树}\)上是可能相连的。
另外，我们知道，一条虚边对应的两个点也显然之间是有边的（废话）。
那么我们可以组合一下，如果 \(x\) 和 \(y\) 在\(\textcolor{green}{原树}\)上的路径上没有多的链，那么也有可能是合法的。那么我们此时先Splay(y)，这样的话，如果满足上面的条件，\(y\) 在\(\textcolor{blue}{辅助树}\)上的父亲绝对是 \(x\)。
当然这样依然不能判断是否有边。如果 \(y\) 在\(\textcolor{blue}{辅助树}\)上有左儿子，那么 \(y\) 所在的实链中，存在在 \(y\) 之上，且不是 \(x\) 的点，那么这样的话，\(x\) 与 \(y\) 之间就存在其他边。

void cut(int x,int y){
    makeroot(x);access(y);
    if(findroot(y)==x&&fa[y]==x&&!son[y][0]) son[x][1]=fa[y]=0;
}

那么我们就只剩下 findroot 这个函数了。

findroot

我们要找 \(x\) 所在的\(\textcolor{green}{原树}\)的根，我们不妨先 access(x) 一下，再 Splay(x) 一下，这样的话，根就和 \(x\) 在同一棵 Splay 中，并且根是这棵 Splay 中深度最小的那个点，直接一直跳左儿子即可。

int findroot(int x){
    access(x);Splay(x);pushdown(x);
    while(son[x][0]) x=son[x][0],pushdown(x);
    Splay(x);
    return x;
}

那么我们 Cut 也就完成了！

一些细节

最后还有一些细节。
比如在 Splay，rotate 操作中，如果当前这个点是这棵 Splay 中的根了，显然不能继续向上了，因此我们需要判断一下一个点是否是其所在的点的根。

isroot

因为\(\textcolor{blue}{辅助树}\)认父不认子的特点，如果一个点既不是其父亲的左儿子，也不是右儿子，那么这个点就是这棵 Splay 的根。

bool isroot(int x){return x!=son[fa[x]][0]&&x!=son[fa[x]][1];}

update

因为我们在进行 Splay 操作的时候，可能其上面的点还有 lazy 标签没有下传，这时如果直接 Splay 就会出问题，此时我们就先从上往下把标签下放即可。

void update(int x){
    if(!isroot(x)) update(fa[x]);
    pushdown(x);
}

为什么在文艺平衡树中不需要 update？因为在找到某个点的时候，其从根到这个点的路径上的标签均被下传过了，而这个点自己的标签又只会往下传，因此不会对 Splay 操作造成影响。

Splay & rotate

那么再然后就是 Splay 函数和 rotate 函数的一点小改动了。

void rotate(int x){
    int y=fa[x],z=fa[y],ch=get(x);
    if(!isroot(y)) son[z][get(y)]=x;
    //这一句要写在前面，因为我们要看y是否已经是根了，不然后面fa[y]改了后，y就一定不是根了。
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    fa[x]=z;fa[y]=x;
    pushup(y);pushup(x);
}

void Splay(int x){
    update(x);
    for(int f=fa[x];f&&!isroot(x);f=fa[x]){
        if(!isroot(f)) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
}

提取路径信息

对于 LCT 的模板题而言，我们还需要维护路径信息，这个怎么实现呢？

我们现在需要维护 \(x\) 到 \(y\) 的路径的一些关系，很自然可以想到先 makeroot(x)，再 access(y)。这样，\(x\) 和 \(y\) 就在同一条实链上了。我们不妨再 Splay(y)。这样，\(x\) 到 \(y\) 的路径就在 \(y\) 的子树中了，这个是很好维护的，我们在 pushup 的时候，顺带记录就好了。
我们称这样提取出一条路径的操作叫做 split。

void split(int x,int y){makeroot(x);access(y);Splay(y);}

对于模板题，我们维护异或和就行。

void pushup(int x){xorsum[x]=xorsum[son[x][0]]^xorsum[son[x][1]]^val[x];}

改变权值

改变权值是容易的，我们先把要改的位置 Splay 一下，再直接改就行了。这样是修改是没有影响的。

void changeval(int x,int y){Splay(x);val[x]=y;}

那么，模板题就结束啦！

// Problem: P3690 【模板】动态树（LCT）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3690
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
const int mod1=1e9+7;
const int mod2=998244353;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

int n,m,tot,son[MAXN][2],fa[MAXN],tag[MAXN],xorsum[MAXN],val[MAXN];

int get(int x){return x==son[fa[x]][1];}
int isroot(int x){return x!=son[fa[x]][0]&&x!=son[fa[x]][1];}
void pushup(int x){xorsum[x]=xorsum[son[x][0]]^xorsum[son[x][1]]^val[x];}
void rev(int x){swap(son[x][0],son[x][1]);tag[x]^=1;}

void pushdown(int x){
    if(tag[x]){
        if(son[x][0]) rev(son[x][0]);
        if(son[x][1]) rev(son[x][1]);
        tag[x]=0;
    }
}

void update(int x){
    if(!isroot(x)) update(fa[x]);
    pushdown(x);
}

void rotate(int x){
    int y=fa[x],z=fa[y],ch=get(x);
    if(!isroot(y)) son[z][get(y)]=x;
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    fa[x]=z;fa[y]=x;
    pushup(y);pushup(x);
}

void Splay(int x){
    update(x);
    for(int f=fa[x];f&&!isroot(x);f=fa[x]){
        if(!isroot(f)) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
}

int access(int x){
    int now=0;
    for(;x;now=x,x=fa[x]) Splay(x),son[x][1]=now,pushup(x);
    pushup(x);
    return now;
}

void makeroot(int x){
    x=access(x);Splay(x);
    swap(son[x][0],son[x][1]);
    tag[x]^=1;
}

int findroot(int x){
    access(x);Splay(x);pushdown(x);
    while(son[x][0]) x=son[x][0],pushdown(x);
    Splay(x);
    return x;
}

void link(int x,int y){
    makeroot(x);Splay(x);
    if(findroot(y)!=x) fa[x]=y;
}

void cut(int x,int y){
    makeroot(x);access(y);
    if(findroot(y)==x&&fa[y]==x&&!son[y][0]) son[x][1]=fa[y]=0;
}

void split(int x,int y){makeroot(x);access(y);Splay(y);}
int query(int x,int y){split(x,y);return xorsum[y];}
void changeval(int x,int y){Splay(x);val[x]=y;}

signed main(){
    read(n,m);
    for(int i=1;i<=n;i++) read(val[i]);
    for(int i=1;i<=m;i++){
        int opt,x,y;
        read(opt,x,y);
        if(opt==0) cout<<query(x,y)<<'\n';
        if(opt==1) link(x,y);
        if(opt==2) cut(x,y);
        if(opt==3) changeval(x,y);
    }
    return 0;
}

应用

我们知道，split 函数将\(\textcolor{green}{原树}\)上的一条路径提取出来了。那我们据此便可以实现很多东西。
比如：维护路径点权和，最大值，最小值之类的。只要这种操作具有交换律和结合律，理论上来讲都是可以维护的。
所以一些LCT的题可以用轻重链剖分解决。

（此处暂时未写）

维护 2-SAT

在某些特殊的 2-SAT 中，我们连的是双向边，此时当然可以使用并查集来维护，但假如我们还需要删除，此时就可以使用 LCT。

例题

P7843 「C.E.L.U-03」布尔

此题题意很显然，给定区间 \([l,r]\)，求最少分割成几段，使得每段的限制条件均有解，输出最小段数。

我们首先来思考一下暴力怎么去做。
有一个很显然的贪心：我们依次加边，如果出现不合法的情况，那么此时断开。这个显然是最优的。
那么我们暴力就可以依次加边，然后跑一次 2-SAT 看是否合法，不合法就将答案加 \(1\)，然后将边清空，继续操作直到边用完。

这样的时间复杂度是 \(O(qn^2)\) 的（设 \(n,m\) 同阶）。可以获得 \(10\) 分。

这样显然是不可行的。我们发现，在这道题中，每次连的边均是双向边。于是我们并不需要使用 2-SAT 来每次暴力判断。我们使用并查集来维护，类似 2-SAT，我们将一个点拆成两个对立点，每次加边后合并一下并查集。如果存在某个点，其对立点处于同一并查集，则此时不合法。 （这种并查集也被称为“种类并查集”。）

此时的时间复杂度降为 \(O(qn\alpha(n))\)，可以获得 \(40\) 分。

如果想要通过，显然不可以每次询问都暴力去做。
我们发现，对于一个位置 \(pos\)，假设其合法的最远位置为 \(a\)，那么 \(\forall b\in [pos,a]\)，区间 \([pos,b]\) 均是合法的。
于是我们记 \(f(i)\) 表示 \(i\) 这个位置合法的最远位置的后一个位置。注意，是后一个位置（虽然不是后一个位置也不是不行）！发现这个东西是可以倍增的！
于是我们现在便可以每次先暴力地求出每个位置的 \(f\) 地值，然后使用倍增来快速回答。

假设我们依然使用并查集来判断合法情况，此时的时间复杂度为 \(O(n^2\alpha(n)+q\log n)\)，似乎也许可以得到 \(70pts\)。

询问的速度已经足够了，我们考虑优化预处理部分。

容易发现，对于 \(f(i)\) 和 \(f(i+1)\)，是存在大量交集的，我们每次暴力去做，显然不优。于是便可以想到使用双指针去扫描。
但是我们的并查集是不允许删除操作的。什么东西又可以连边又可以删边呢？LCT 可以。于是我们现在就来仔细想想 LCT 怎么去实现这个预处理。

我们令当前的区间为 \([l,r]\)，我们此时需要将 \(r\) 进行扩展，需要连接 \(u\) 和 \(v\) 两个点。我们分两种情况来讨论。

1. 连接 \(u\) 和 \(v\) 后没有出现环，那么直接连接即可。
   
2. 连接 \(u\) 和 \(v\) 后出现了环，理论上来说我们随便断开一条边，是不会影响到连通性的，但是我们后面可能需要将 \(l\) 往前挪，此时需要删除编号为 \(l\) 的边。如果我们前面随意删除了一条边，此时又删去了 \(l\) 这条边，可能导致原本应该连通的图变得不连通。那么我们就删去编号最小的边，这样就没有影响了。

将 \(r\) 扩展后，我们此时需要判断是否合法，从而决定 \(l\) 点是否需要往前挪。
我们不可能 \(O(n)\) 的去遍历每个点看是否合法，这样的时间复杂度是 \(O(n\log n)\) 的，还不如并查集。
但是我们又发现连接了一条边后，出现冲突的位置是不确定的。
思考一下，发现我们将前面连接的边，对于其对立点，我们也连边，假如没有出现冲突，这两部分会是独立的。而假如出现冲突，则一定是因为这条边的假如而冲突，那么也就是连接的这条边的两端点出现了冲突。这样我们只需要判断一次即可知道是否出现冲突。

那么基本也就结束了，时间复杂度 \(O(n\log n+q\log n)\)，常数较大，但是是可以通过的。
细节有点多，具体可以看代码。

// Problem: P7843 「C.E.L.U-03」布尔
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7843
// Memory Limit: 256 MB
// Time Limit: 2500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1.5e6+10;
const int mod1=1e9+7;
const int mod2=998244353;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
    x=0;
    bool f=false;
    char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
    read(x),read(y...);
}

bool awa;
int n,m,q,l,r,cnt,e_cnt,tag[MAXN],fa[MAXN],son[MAXN][2],val[MAXN],minval[MAXN],f[MAXN][21];
int U[MAXN],X[MAXN],V[MAXN],Y[MAXN];

bool get(int x){return x==son[fa[x]][1];}
bool isroot(int x){return x!=son[fa[x]][0]&&x!=son[fa[x]][1];}
void rev(int x){swap(son[x][0],son[x][1]);tag[x]^=1;}
void pushup(int x){minval[x]=min({val[x],minval[son[x][0]],minval[son[x][1]]});}

void pushdown(int x){
    if(tag[x]){
        if(son[x][0]) rev(son[x][0]);
        if(son[x][1]) rev(son[x][1]);
        tag[x]=0;
    }
}

void update(int x){
    if(!isroot(x)) update(fa[x]);
    pushdown(x);
}

void rotate(int x){
    int y=fa[x],z=fa[y],ch=get(x);
    if(!isroot(y)) son[z][get(y)]=x;
    son[y][ch]=son[x][ch^1];
    if(son[x][ch^1]) fa[son[x][ch^1]]=y;
    son[x][ch^1]=y;
    fa[y]=x;fa[x]=z;
    pushup(y);pushup(x);
}

void Splay(int x){
    update(x);
    for(int f=fa[x];!isroot(x);f=fa[x]){
        if(!isroot(f)) rotate(get(x)==get(f)?f:x);
        rotate(x);
    }
}

int access(int x){
    int pos=0;
    for(;x;pos=x,x=fa[x]) Splay(x),son[x][1]=pos,pushup(x);
    pushup(x);
    return pos;
}

void makeroot(int x){x=access(x);Splay(x);rev(x);}

int findroot(int x){
    access(x);Splay(x);pushdown(x);
    while(son[x][0]) x=son[x][0],pushdown(x);
    Splay(x);return x;
}

void link(int x,int y){
    makeroot(x);Splay(x);
    if(findroot(y)!=x) fa[x]=y;
}

void cut(int x,int y){
    makeroot(x);access(y);
    if(findroot(y)==x&&fa[y]==x&&!son[y][0]) fa[y]=son[x][1]=0;
}

void split(int x,int y){makeroot(x);access(y);Splay(y);}
void change(int pos,int z){Splay(pos);val[pos]=z;pushup(pos);}

void get(int &x1,int &y1,int &x2,int &y2,int &id1,int &id2,int i){
    id1=i+2*n;id2=i+2*n+m;
    if(X[i]^Y[i]) x1=U[i],y1=V[i]+n,x2=U[i]+n,y2=V[i];
    else x1=U[i],y1=V[i],x2=U[i]+n,y2=V[i]+n;
}

bool t(int x,int y){
    return findroot(x)==findroot(y);
}
bool qwq;

signed main(){
    // cout<<(&awa-&qwq)/1024.0/1024.0<<endl;
    read(n,m,q);cnt=n;
    for(int i=0;i<=2*n+2*m;i++) val[i]=minval[i]=1e9;
    l=r=1;
    for(int i=1;i<=m;i++,r++){
        read(U[i],X[i],V[i],Y[i]);
        int x1,x2,y1,y2,id1,id2;
        get(x1,y1,x2,y2,id1,id2,i);
        if(t(x1,y1)){
            split(x1,y1);
            int minedge=minval[y1];
            int xx,yy,XX,YY,ID1,ID2;
            get(xx,yy,XX,YY,ID1,ID2,minedge);
            cut(xx,ID1);cut(ID1,yy);
            cut(XX,ID2);cut(ID2,YY);
        }
        change(id1,i);
        link(x1,id1);link(id1,y1);
        while(t(x1,x2)){
            f[l][0]=r;
            int xx,yy,XX,YY,ID1,ID2;
            get(xx,yy,XX,YY,ID1,ID2,l);
            cut(xx,ID1);cut(ID1,yy);
            cut(XX,ID2);cut(ID2,YY);
            l++;
        }
        change(id2,i);
        link(x2,id2);link(id2,y2);
    }
    for(;l<=m;l++) f[l][0]=m+1;
    for(int i=m;i>=1;i--) for(int j=1;j<21;j++) f[i][j]=f[f[i][j-1]][j-1];
    for(int i=1;i<=q;i++){
        int l,r,ans=0;
        read(l,r);
        for(int j=20;j>=0;j--){
            if(f[l][j]>0&&f[l][j]<=r+1){
                ans+=(1<<j);
                l=f[l][j];
            }
        }
        if(l!=r+1){
            for(int j=0;j<=20;j++){
                if(f[l][j]>=r+1){
                    ans+=(1<<j);
                    break;
                }
            }
        }
        if(f[l][0]==l){
            cout<<-1<<'\n';
            continue;
        }
        cout<<ans<<'\n';
    }
    return 0;
}