今天下午学长刚讲了交互题,写完交上去一发过,似乎还是最优解?
题目传送门
题意简述
有 \(n\) 种物品,每种有 \(m\) 个,现在这些物品被随机打乱了(你并不知道顺序)。你每次可以选择任意多个(即给出一个向量)进行询问,每次询问会告诉你这些物品中 \(1\) 到 \(n\) 这 \(n\) 种物品中,最少的那种物品的数量。最后你需要给出 \(m\) 个完全不同的向量,每个向量必须包含这 \(n\) 种物品,每种物品有且仅有 \(1\) 个,在不多于 \(50000\) 次询问下完成。
思路
注意到只能在 \(50000\) 次询问内完成,而物品最多有 \(n \times m\) 共 \(10000\) 个,最后对于每个物品,我们还剩下了 \(5\) 次查询机会。因为 \(m \le 25\),所以 \(\log m < 5\),因此我们可以考虑二分(这个其实还是比较难想的?)
我们令 \(M\) 表示当前处理的需要提交的向量的数量,\(mid\) 变量表示二分的值,即$mid = $所以当 \(M=1\) 的时候,我们就可以提交当前这一个向量。我们每次将一个大向量从前往后一个个遍历(具体方法后面会讲),将其拆成两个小向量,再递归处理,递归到最后直接提交答案,可以计算最多需要询问 \(43600\) 次,时间复杂度也是 \(O(n \log m)\) 的,可以通过。
实现
最开始,我们将 \(n \times m\) 这么多个数全部扔进一个叫做 \(x\) 的向量中,我们要将 \(x\) 这个向量拆成两个小的向量 \(y\) 和 \(z\)。使得 \(y\) 这个向量中有 \(mid\) 串未处理的物品,\(z\) 中有 \(M-mid\) 串未处理的物品。
根据查询的性质:返回 \(1\) 到 \(n\) 这 \(n\) 种物品中最少的一种物品的数量。因此一个向量可以组成多少个串,就是对这个向量进行询问后的返回值。
因此我们从 \(x\) 这个向量的第一个元素开始遍历,假如去掉这一个物品后,我们进行一次查询,发现返回值仍是大于等于 \(mid\) 的,那么就说明,去掉这个物品后,剩下的物品也至少也可以组成 \(mid\) 个串,那么这个物品就可以扔到 \(z\) 这个向量。反之当返回值小于 \(mid\) 的时候,就说明去掉这个物品后,剩下的物品不能够组成 \(mid\) 个串,因此这个物品是必须的,需要放到 \(y\) 向量。再依次对 \(y\) 和 \(z\) 递归处理,当一个向量长度为 \(n\) 时,那么就说明这是一个合法的串,提交答案即可。
注意! 当去掉这个物品后,剩下的物品不能组成至少 \(mid\) 根串的时候,我们是需要把它扔进 \(y\) 这个向量的,但是它依然应该被保留在 \(x\) 这个向量中,否则在后面继续遍历的时候,无论如何返回的询问值总是小于 \(mid\) 的。因此在代码实现的时候,我们其实并不需要真的开两个向量,自然的当 \(x\) 中可以扔去 \(z\) 的扔完后,剩下的其实就是原先\(y\) 这个向量。
具体的,我们维护一个 \(pos\) 变量,记录当前应该取的是 \(x\) 这个向量中的哪个元素的位置,再另开一个变量记录一下这个元素的值。因为我们有时需要扔进另一个向量,有时需要继续保留。每次我们先将这个元素从向量中弹出,进行查询后根据返回值决定要放回去还是丢进另一个变量。在扔走的时候,\(pos\) 是不变的,当留下的时候,将 \(pos\) 增加 \(1\)。
具体可以看下面几张图来理解: 
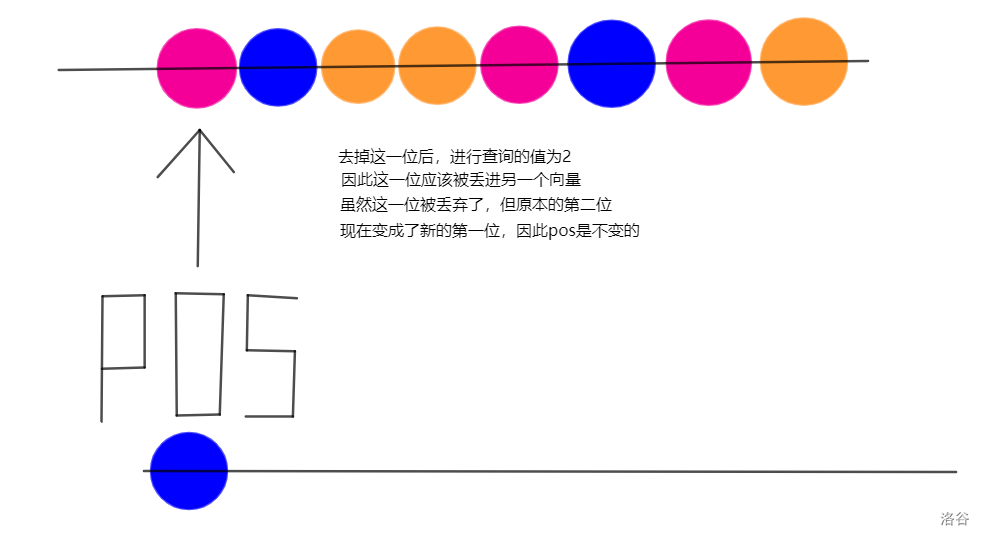
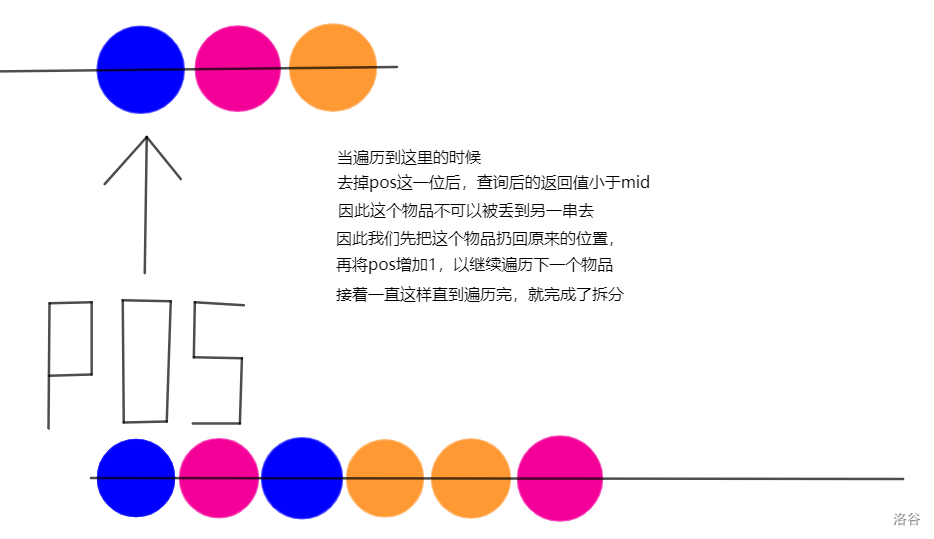
为什么这样是正确的?因为我们在每次处理 \(x\) 这个向量时,都保证了处理后的 \(y\) 向量和 \(z\) 向量中,分别可以组合出 \(mid\) 个串和 \(M-mid\) 个串。当最后 \(M=1\) 的时候,也就自然的一定可以组合出 \(1\) 个串,因此这也就是答案。
最后处理一些细节,代码也很容易完成,似乎是最短的,就可以愉快地 AC 啦~
代码
#include <vector>
void Solve(int N, int M);
int Query(const std::vector<int> &x);
void Answer(const std::vector<int> &a);
void work(std::vector<int> &a,int m){//递归处理
if(m==1){//得到答案
Answer(a);
return;
}
int mid=m/2,cache;
std::vector<int> x;
int pos=0;
int len=a.size();
for(int i=1;i<=len;i++){
cache=a[pos];
a.erase(a.begin()+pos);
if(Query(a)<mid) a.insert(a.begin()+pos,cache),pos++;//返回值大于等于mid,扔进另一个向量
else x.push_back(cache);//返回值小于mid,需要扔回去
}
work(a,mid);
work(x,m-mid);//向下递归继续处理
}
void Solve(int N,int M){
std::vector<int> s;
for(int i=1;i<=N*M;i++) s.push_back(i);//将最开始的N*M个数全部丢进一个初始向量
work(s,M);
}